오늘은 그래프 탐색에 속하는 깊이 우선 탐색(DFS)와 너비 우선 탐색(BFS)에 대해서 공부하였다.
우선 그래프를 만드는 방법을 matrix(매트릭스)로 표현을 해보겠다.
package ch04.graph;
public class UndirectedGraph{
private int count; //노드 수
private int[][] vertexMatrix; // matrix로 그래프 표시
public UndirectedGraph(int count){
this.count = count;
vertexMatrix = new int[count][count];
}
public void addEdges(int from, int to, int weight){
vertexMatrix[from][to] = weight;
vertexMatrix[to][from] = weight;
}
public int[][] getMatrix(){
return vertexMatrix;
}
}이런식으로 그래프를 만들 수 있다. 무방향 그래프일 때는 vertexMatrix[from][to] = weight; 와 vertexMatrix[to][from] = weight;를 두번 써주면 되고 방향이 있는 그래프는 이렇게 작성하면 안된다.
다음으로는 아래의 사진에 대해서 깊이 우선 탐색(DFS)먼저 구현 해보겠다.
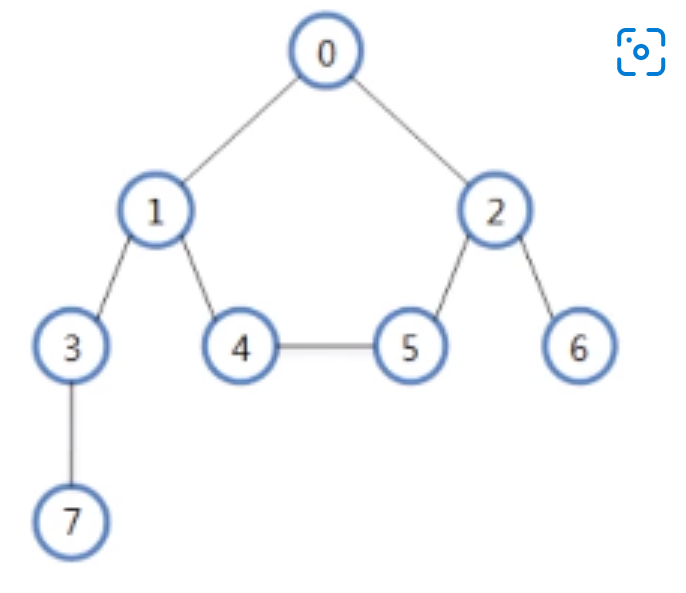
● 연결한 노드를 우선 탐색 하는 방식
● 스택을 활용하여 구현할 수 있음
● DFS 탐색 순서 : 0 - 1 - 3 - 7 - 4 - 5 - 2 - 6 or 0 - 2 - 6 - 5 - 4 - 1 - 3 - 7
package ch04.dfs;
import java.util.Stack;
import ch04.graph.UndirectedGraph;
public class DfsSearch {
int count;
boolean[] visited;
Stack<Integer> stack;
int[][] matrix;
public DfsSearch(int count){
this.count = count;
visited = new boolean[count];
stack = new Stack<Integer>();
}
public void bfsTraversal() {
stack.push(0);
visited[0] = true;
while(stack.size() != 0) {
int node = stack.pop();
System.out.print(node + " ");
for(int j = 0; j<count; j++) {
if(matrix[node][j] != 0 && !visited[j] ) {
stack.push(j);
visited[j] = true;
}
}
}
}
public static void main(String[] args) {
int count = 8;
UndirectedGraph graph = new UndirectedGraph(count);
DfsSearch dfsSearch = new DfsSearch(count);
graph.addEdges(0, 1, 1);
graph.addEdges(0, 2, 1);
graph.addEdges(1, 3, 1);
graph.addEdges(1, 4, 1);
graph.addEdges(2, 5, 1);
graph.addEdges(2, 6, 1);
graph.addEdges(4, 5, 1);
graph.addEdges(3, 7, 1);
dfsSearch.matrix = graph.getMatrix();
dfsSearch.bfsTraversal();
}
}구현 결과

다음으로는 위의 사진에 대해 너비 우선 탐색(BFS)를 구현 해보겠다.
● 한 노드에 모든 인접한 노드를 탐색하는 방식
● 큐를 활용하여 구현할 수 있음
● BFS 탐색 순서 : 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7
package ch04.bfs;
import java.util.ArrayList;
import ch04.graph.UndirectedGraph;
public class BfsSearch {
int count;
boolean[] visited;
ArrayList<Integer> queue;
int[][] matrix;
public BfsSearch(int count){
this.count = count;
visited = new boolean[count];
queue = new ArrayList<Integer>();
}
public void bfsTraversal() {
queue.add(0);
visited[0] = true;
while(queue.size() != 0) {
int node = queue.remove(0);
System.out.print(node + " ");
for(int j = 0; j<count; j++) {
if(matrix[node][j] != 0 && !visited[j] ) {
queue.add(j);
visited[j] = true;
}
}
}
}
public static void main(String[] args) {
int count = 8;
UndirectedGraph graph = new UndirectedGraph(count);
BfsSearch bfsSearch = new BfsSearch(count);
graph.addEdges(0, 1, 1);
graph.addEdges(0, 2, 1);
graph.addEdges(1, 3, 1);
graph.addEdges(1, 4, 1);
graph.addEdges(2, 5, 1);
graph.addEdges(2, 6, 1);
graph.addEdges(4, 5, 1);
graph.addEdges(3, 7, 1);
bfsSearch.matrix = graph.getMatrix();
bfsSearch.bfsTraversal();
}
}구현 결과
다음 으로는 그래프 탐색을 이용해 최단거리 구하기 문제를 구현 해보겠다.
5. 최단거리 구하기
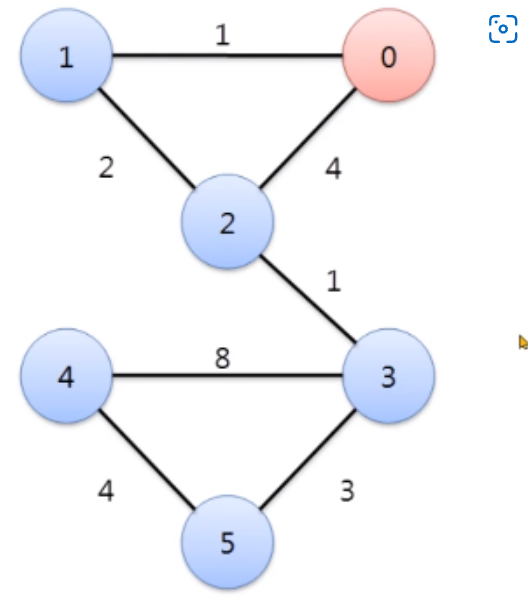
문제 풀이
● 모든 노드 중 연결된 최단거리를 가진 노드를 찾아서
● 큐를 활용하여 구현할 수 있음
● 노드 v에 인접한 노드 w에 대해 다음 조건이 성립하면 w에 대한 최단 거리를 업데이트 한다.
(즉 원래 w로 가던 거리보다 v를 거쳐 가는 거리가 더 가까우면 w로 가는 거리를 v를 거쳐가는 것으로 최단 거리를 수정)
Yw = Yv + Cvw if Yv + Cvw < Yw
문제 풀이 코드
package ch05;
class MyGraph{
private int count; //노드 수
private int[][] vertexMatrix; // matrix로 그래프 표시
private int[] distance; // 특정 노드에 대한 각 노드의 최단 거리
private boolean[] visited; // alread visited???
private static int UNLIMIT = 999999999; // 초기값
public MyGraph(int count){
this.count = count;
vertexMatrix = new int[count][count];
distance = new int[count];
visited = new boolean[count];
}
public void addEdges(int from, int to, int weight){
vertexMatrix[from][to] = weight;
vertexMatrix[to][from] = weight;
}
public void calcShotestPath(int from){
for(int i=0;i<count;i++){
distance[i] = UNLIMIT;
}
visited[from] = true;
distance[from] = 0;
//연결노드 distance갱신
for(int i= 0; i<count; i++){
if(visited[from] && vertexMatrix[from][i] !=0){
distance[i] = vertexMatrix[from][i];
}
}
for(int k =0; k<count-1; k++){
int min=UNLIMIT;
int minIndex= -1;
for(int i = 0; i< count ;i++){
if(!visited[i] && distance[i]!=UNLIMIT){
if(distance[i] < min ){
min = distance[i];
minIndex = i;
}
}
}
visited[minIndex] = true;
for(int i=0; i<count; i++){
if(!visited[i] && vertexMatrix[minIndex][i]!=0){
if(distance[i]>distance[minIndex]+vertexMatrix[minIndex][i]){
distance[i] = distance[minIndex]+vertexMatrix[minIndex][i];
}
}
}
}
}
public void showDistance(int from) {
for(int i = 0; i<count; i++) {
System.out.println(from + " 노드로부터 " + i + " 노드의 최단 거리는 : " + distance[i]);
}
}
}
public class ShortestPath {
public static void main(String[] args) {
MyGraph graph = new MyGraph(6);
graph.addEdges(0, 1, 1);
graph.addEdges(0, 2, 4);
graph.addEdges(1, 2, 2);
graph.addEdges(2, 3, 1);
graph.addEdges(3, 4, 8);
graph.addEdges(3, 5, 3);
graph.addEdges(4, 5, 4);
graph.calcShotestPath(1);
graph.showDistance(1);
}
}문제 풀이 결과

오늘 공부한 내용은 여기까지 이다. 코딩테스트에 대해 알아보면 그래프 문제가 제일 어렵다고 하는데 왜 어려운지 알게 되었다.. 이론은 이해가 되는데 코드적으로 코딩을 하려 해보면 뇌정지가 오는거 같다.. 연습을 좀 많이 해야할거 같다는 생각이 들면서 오늘의 공부는 여기서 마치겠다. 다음 글에서는 저번에 공부하다가 말았던 웹 개발 이론에 대해서 마무리를 하고 본격적으로 Spring에 대해서 공부를 하겠다.
그럼 20000 ~~

'코딩테스트' 카테고리의 다른 글
| 정렬 알고리즘(java) (0) | 2023.04.26 |
|---|---|
| 정렬된 수에서 하나의 수의 위치 찾기(java) (0) | 2023.04.26 |
| 나열된 수에서 최솟값과 최대값 구하기 문제풀이(java) (0) | 2023.04.21 |